Courses by Software
Courses by Semester
Courses by Domain
Tool-focused Courses
Machine learning
POPULAR COURSES
Success Stories
Curve fitting
1.AIM: To perform a curve fitting for the given dataset and to find the best fit and perfect fit for that particular dataset using MATLAB. 2.OBJECTIVES OF THE PROJECT: Write code to fit a linear and cubic polynomial for the Cp data. Plot the linear and cubic fit curves along with the raw data points. Title and axes…
Amit Chilap
updated on 15 Feb 2021
1.AIM:
- To perform a curve fitting for the given dataset and to find the best fit and perfect fit for that particular dataset using MATLAB.
2.OBJECTIVES OF THE PROJECT:
- Write code to fit a linear and cubic polynomial for the Cp data.
- Plot the linear and cubic fit curves along with the raw data points. Title and axes labels are a must, legends could be shown if necessary.
- Write a code to show the split-wise method.
- Explain the parameters used to measure the fitness characteristics for both curves.
3.THEORY & GOVERNING EQUATIONS:
What is Curve Fitting?
Curve fitting is the process of constructing a curve or mathematical function, that has the best fit to a series of data points, possibly subject to constraints. Curve fitting can involve either interpolation, where an exact fit to the data is required, or smoothing, in which a "smooth" function is constructed that approximately fits the data. It is highly effective in the mathematical modeling of some natural processes. Fitted curves can be used as an aid for data visualization, to infer values of a function where no data are available, and to summarize the relationships among two or more variables Extrapolation refers to the use of a fitted curve beyond the range of the observed data and is subject to a degree of uncertainty since it may reflect the method used to construct the curve as much as it reflects the observed data.
Curve Fitting in MATLAB
MATLAB has two functions, polyfit and polyval, which can quickly and easily fit a set of data points with a polynomial.
Here, the coefficients are the a1, a2.
If you had a straight line, then n = 1, and the equation would be,f(x)=a1x+a2 .
We can see that if f(x) was called y and a1 was called "m" and a2 was called "b" that we would have the familiar equation for a straight line: y = mx + b.
Thus, a straight line is a first-degree polynomial equation. The reason the degree is equal to one is that the "x” in the equation is raised to the power of one it has an exponent of one.
There is another type of polynomials.
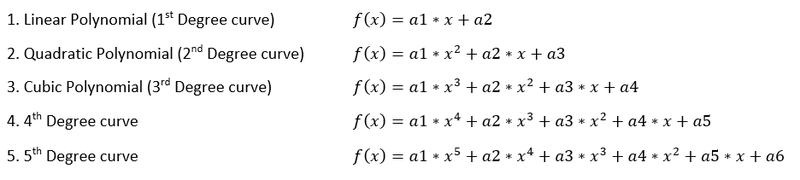
Assume data points (x1,y1),(x2,y2),(x3,y3),...(xn,yn) and assume the best fit for these set of points will be y = f(x), the criterion under which the equation of the curve will be the best fit possible is as follows.

Suppose each of these n points has an individual error (difference in y co-ordinate values)
The error for a general "i" point can be given by the function,
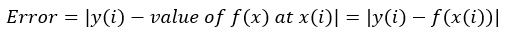
To remove the modulus sign, it is effective if we square the error term, when we square the error terms and add the errors for all the "n" points we get,
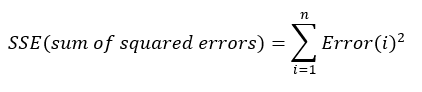
assume the proposed equation is an nth degree polynomial of the form,
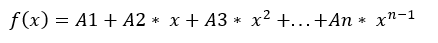
When we differentiate the SSE with each and every coefficient of the proposed equation f(x) and equate it to zero, we can find the minima and value of that coefficient.

Upon solving the multiple systems of equations, we can find the values of all the coefficients.
This method is known as the Least Squares Method and is the most commonly used technique as long as the fitting function is a polynomial.
How to choose the best fit?
Upon finding a curve that satisfies the data points 4 quantities help us measure the goodness of fit criteria or how well the equation is representing the data points. There are,
- The sum of squares due to error (SSE)
- R-square
- Adjusted R-square
- Root mean squared error (RMSE)
The first quantity SSE was already measured in the previous section of this article.
- R-square
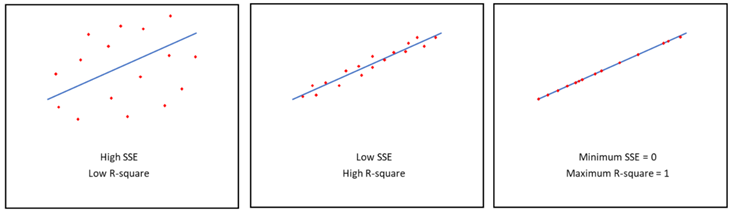
This quantity measures how successful the fit is in explaining the variation of the data. Put another way. R-square is the square of the correlation between the response values and the predicted response values. It is also called the square of the multiple correlation coefficient and the coefficient of multiple determination.
What that means in layman's terms is that the higher the value of R - square the better the fit, the lower it is the lousier the fit, R-square ranges from a value of O to 1
- 0 for the worst possible fit for the data set
- 1 for the best possible fit for the data set
The value of R-square can be calculated using the following formula
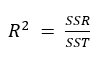
where,
SSR = sum of squares of the regression, which is the square of the difference between the value of the fitting function at a given point and the arithmetic mean of the data set.

if y = f(x) is the fit curve then the SSR is defined as follows,
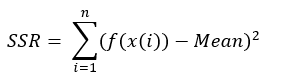
Similarly, SSE is defined as follows,
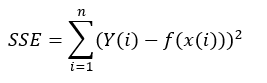
Now the term SST is given by the summation of SSR and SSE
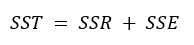
From here, we can calculate the value of R2.
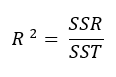
- Adjusted R-square
Adjusted R-square is a normalizing variation of R-square which neglects the variation of R-square due to insignificant independent variables.
for, y=f(x1,x2,x3,...,xn), here, x1,x2,...,xn are the independent variables and is the dependent variable.
Adjusted R-square disregards these infinitesimally small increments to R-square, and only considers the variables which contribute to the output of the system drastically.
R-square is formulated as shown below,
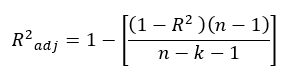
where,
n- the number of data points
k- the number of independent variables
- RMSE (Root Mean Squared Error)
This statistic is also known as the fit standard error and the standard error of the regression. It is an estimate of the standard deviation of the random component in the data, and is defined as,
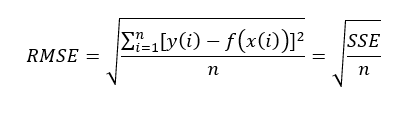
Where “n” is the total number of data points available.
4.BODY OF THE CONTENT:
- MATLAB Programming language is used.
- Performing Linear & Cubic Curve Fitting Program is attached below.
- File Name: Performing_Curve_Fitting.m
%OBJECTIVES OF THE PROJECT:
%Write code to fit a linear and cubic polynomial for the Cp data.
%Plot the linear and cubic fit curves along with the raw data points. Title and axes labels are a must, legends could be shown if necessary.
%Write a code to show the split-wise method.
%Explain the parameters used to measure the fitness characteristics for both curves.
close all
clear all
clc
cp_data =load('data'); %Loading the Data File.
temp=cp_data(:,1); %Collecting Temperature Data from Data File.
cp=cp_data(:,2); %Collecting CP Data from Data File.
% Linear Predicted Curve
% cp=a*t+b
coeff_L = polyfit(temp,cp,1); %in build "polyfit()" command is used to find coefficients for Linear Predicted Curve.
Predicted_Cp_L=polyval(coeff_L,temp); %in build "polyval()" command is used to solve and collect CP Data for Linear Predicted Curve.
% Cubic Predicted Curve
% cp=a*t^3+b*t^2+c*t+d
coeff_C = polyfit(temp,cp,3); %in build "polyfit()" command is used to find coefficients for Cubic Predicted Curve.
Predicted_Cp_C=polyval(coeff_C,temp); %in build "polyval()" command is used to solve and collect CP Data for Cubic Predicted Curve.
% Calculation of Goodness of Fit.
% 1.The sum of squares due to error(SSE).
for i=1:length(cp); %Using FOR loop to calculate errors at every value for Predicted Curve.
sse_L(i)=(cp(i)-Predicted_Cp_L(i))^2; %Calculating errors at every value for Linear Predicted Curve.
sse_C(i)=(cp(i)-Predicted_Cp_C(i))^2; %Calculating errors at every value for Cubic Predicted Curve.
end %Ending 'for' function.
SSE_L=sum(sse_L); %Summations of errors of each value of Linear Predicted Curve.
SSE_C=sum(sse_C); %Summations of errors of each value of Cubic Predicted Curve.
% 2.R-Square.
for i=1:length(cp); %Using FOR loop to calculate errors at every value for Predicted Curve.
ssr_L(i)=(Predicted_Cp_L(i)-(sum(cp)/length(cp)))^2; %Calculating SSR every value for Linear Predicted Curve.
ssr_C(i)=(Predicted_Cp_C(i)-(sum(cp)/length(cp)))^2; %Calculating SSR every value for Cubic Predicted Curve.
end %Ending 'for' function.
SSR_L=sum(ssr_L); %Summations of SSR of each value of Linear Predicted Curve.
SST_L=SSE_L+SSR_L; %Calculating SST of Linear Predicted Curve.
Rsq_L=SSR_L/SST_L; %Calculating R-Square value of Linear Predicted Curve.
SSR_C=sum(ssr_C); %Summations of SSR of each value of Cubic Predicted Curve.
SST_C=SSE_C+SSR_C; %Calculating SST of Cubic Predicted Curve.
Rsq_C=SSR_C/SST_C; %Calculating R-Square value of Cubic Predicted Curve.
% 3.Adjusted R-Square.
k_L=length(coeff_L)-1; %Calculating independent variables in Linear Predicted Curve.
Rsq_adj_L=1-[(1-Rsq_L^2)*(length(cp)-1)/(length(cp)-k_L-1)]; %Calculating Adjusted_R-Square value of Linear Predicted Curve.
k_C=length(coeff_C)-1; %Calculating independent variables in Cubic Predicted Curve.
Rsq_adj_C=1-[(1-Rsq_C^2)*(length(cp)-1)/(length(cp)-k_C-1)]; %Calculating Adjusted_R-Square value of Cubic Predicted Curve.
% 4.Root mean square error(RMSE).
RMSE_L=(SSE_L/length(cp))^(0.5); %Calculating RMSE value of Linear Predicted Curve.
RMSE_C=(SSE_C/length(cp))^(0.5); %Calculating RMSE value of Cubic Predicted Curve.
% Putting Errors in form of an Table
error_names = {'SSE';'R-Square';'Adjusted R-Sqaure'; 'RMSE'}; %Title of goodness of curve fit.
Linear_Predicted_Curve=[SSE_L;Rsq_L;Rsq_adj_L;RMSE_L]; %Creating matrix of goodness of curve fit of Linear Predicted Curve.
Cubic_Predicted_Curve=[SSE_C;Rsq_C;Rsq_adj_C;RMSE_C]; %Creating matrix of goodness of curve fit of Cubic Predicted Curve.
disp('Goodness Parameter for Linear and Cubic Curve fit') %Title of Table.
Goodness_Parameters = table(Linear_Predicted_Curve,Cubic_Predicted_Curve,'RowNames',error_names) %Creating Goodness of Curve Fit Table.
% Plotting the CURVES
hold on %Command to add multiple Plots in single Figure.
plot(temp,cp,'color','g','linewidth',5) %Plotting Original Data Curve.
plot(temp,Predicted_Cp_L,'color','r','linewidth',3) %Plotting Linear Predicted Curve.
plot(temp,Predicted_Cp_C,'color','b','linewidth',3) %Plotting Cubic Predicted Curve.
txt1='The Goodness of Fit of'; %Text to display on plot.
txt2='Linear Predicted Curve'; %Text to display on plot.
txt3=sprintf('SSE %1.4f',SSE_L); %Text to display SSE of Linear Predicted Curve on plot.
txt4=sprintf('R^2 %1.4f',Rsq_L); %Text to display R^2 of Linear Predicted Curve on plot.
txt5=sprintf('Adjusted R^2 %1.4f',Rsq_adj_L); %Text to display Adjusted_R^2 of Linear Predicted Curve on plot.
txt6=sprintf('RMSE %1.4f',RMSE_L); %Text to display RMSE of Linear Predicted Curve on plot.
txtL={txt1,txt2,txt3,txt4,txt5,txt6}; %Text to display Goodness of Fit of Linear Predicted Curve on plot.
text(1500,1000,txtL,'HorizontalAlignment','center'); %Position & Text to display Goodness of Fit of Linear Predicted Curve on plot.
txt7='The Goodness of Fit of'; %Text to display on plot.
txt8='Cubic Predicted Curve'; %Text to display on plot.
txt9=sprintf('SSE %1.4f',SSE_C); %Text to display SSE of Cubic Predicted Curve on plot.
txt10=sprintf('R^2 %1.4f',Rsq_C); %Text to display R^2 of Cubic Predicted Curve on plot.
txt11=sprintf('Adjusted R^2 %1.4f',Rsq_adj_C); %Text to display Adjusted_R^2 of Cubic Predicted Curve on plot.
txt12=sprintf('RMSE %1.4f',RMSE_C); %Text to display RMSE of Cubic Predicted Curve on plot.
txtC={txt7,txt8,txt9,txt10,txt11,txt12}; %Text to display Goodness of Fit of Cubic Predicted Curve on plot.
text(3000,1000,txtC,'HorizontalAlignment','center'); %Position & Text to display Goodness of Fit of Cubic Predicted Curve on plot.
xlabel('Temperature [K]') %Labelling X-Axis.
ylabel('Specific Heat (Cp) [KJ/(kg*K)') %Labelling Y-Axis.
legend('Orignal Curve','Linear Predicted Curve','Cubic Predicted Curve','location','northwest') %Adding Legends on Plot.
- Explanation/Workflow for Performing Curve Fitting.
- The program starts with loading all the data into a variable called cp_data from the file called data which stores data for Cp at various temperatures.
- For the curve fitting the two commands are used, the ployfit and polyval commands.
- The command polyfit returns the coefficients in the equation like considering the equation
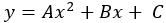 , here the coefficients A, B, and C are calculated.
, here the coefficients A, B, and C are calculated.
- The degree of the polynomial is chosen based on the goodness of the fit.
- Based on the degree of the polynomial the number of the coefficients also changes and their values also change.
- The command polyval returns the predicted value of Cp based on the coefficients calculated.
- We calculate the predicted Cp for both linear and cubic degree of the polynomial
- We calculate the goodness parameters SSE, R-Square, Adjusted R-Square, and RMSE for both the curves fit and display the parameters in form of a table and also going to display on the plot.
- The graph is plotted for the original and predicted values using a linear and cubic degree of the polynomial
- Then we compare all the plots (Original Curve, Linear Predicted Curve, Cubic Predicted Curve).
- Also, to check the goodness of fit the curve fitting app is used from the apps section. The required data is provided like a name. X data, Y data, polynomial, the degree of the polynomial is filled and output containing the graph coefficients and goodness of fit data is obtained.
- Step-Wise Explanation is provided in the code by using next to its comments.
- Results
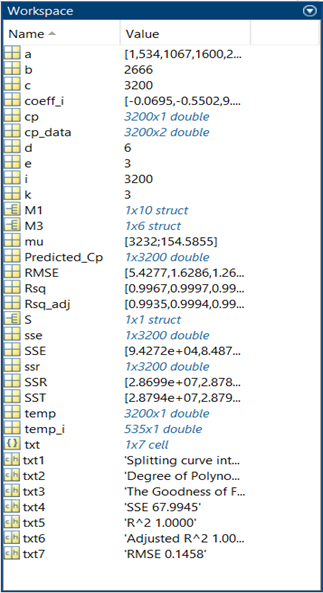
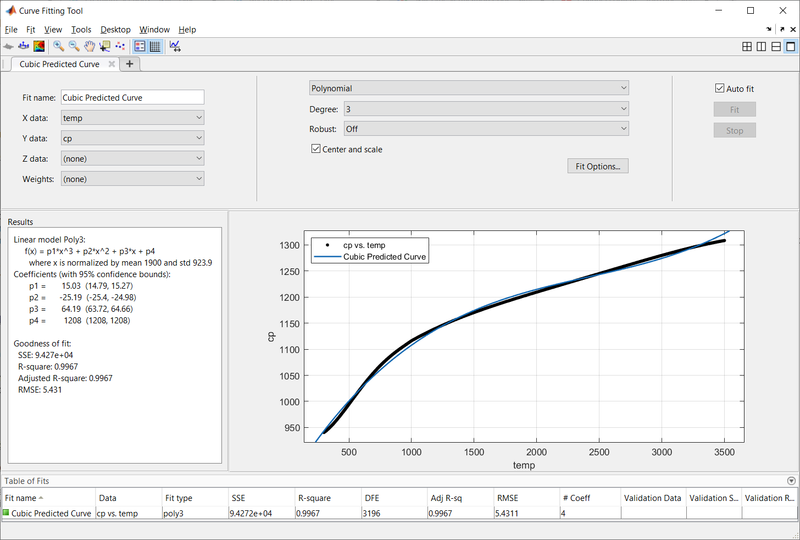
Using the Curve fitting toolbox in MATLAB to validate your fitness characteristics.
- Linear Predicted Curve Fit.

- Cubic Predicted Curve Fit.
Based on the research you have done, answer the following questions:
- How to make a curve fit perfectly?
- We have to find out the error during curve fitting and curve fit can be made perfect by interpolating the datasets.
- By interpolation, the errors can be minimized and it is also possible to reduce the errors to zero.
- Curve fit should match with the original data without showing the error in command windows.
- For setting the curve here, we eliminate the error by using the center and scaling code, i.e., elimination of error is done through “S” & “mu” for 3rd-degree polynomial or cubic curve.
- Hereby increasing the order of polynomial OR by splitting the curve with more sections we can make the predicted curve more/perfectly fit.
- The perfect fit means the curve should fit the original curve without showing any errors in that particular degree of the polynomial. This means that every data point in the original plot should be on the curve.
- The perfect fit can always be the best fit but the best fit cannot be a perfect fit.
- We can fit a curve perfectly only by using interpolation. We do not need to get a single function representing a complete trend.
- How to get the best fit? Note: Best fit and the perfect fit are two completely different phenomena.
- Best fit" simply means that the differences between the actual measured Y values and the predicted Y values by the model equation are minimized.
- It does not mean a "perfect" fit; in most cases, a least-squares best fit does not go through all the points in the data set. Above all, a least-squares fit must conform to the selected model
- We can get the best fit by
- Using higher degree polynomial.
- Using split wise curve fitting
- To compare the accuracy of curve fit, we can evaluate the goodness parameter. Once the improvement in the goodness parameter becomes stagnant, the best fit curve is obtained.
- What could be done to improve the cubic fit?
- To improve the cubic fit, we can do the split-wise fitting for the curve.
- That is splitting the curve into multiple parts and using a different cubic polynomial for different sets of temperature and specific heat values.
- This reduces the errors and the best fit is obtained.
- Here I have Split the data from 1 to 10 sections and performed a split fitting for the cubic function.
- Supplementary Programs
- Performing Best Curve Fit by Using Higher Degree Polynomial Program is attached below.
- File Name : Best_Curve_Fit_by_Poly_Degree.m
%OBJECTIVES OF THE PROJECT:
%Write code to fit a linear and cubic polynomial for the Cp data.
%Plot the linear and cubic fit curves along with the raw data points. Title and axes labels are a must, legends could be shown if necessary.
%Write a code to show the split-wise method.
%Explain the parameters used to measure the fitness characteristics for both curves.
close all
clear all
clc
cp_data =load('data'); %Loading the Data File.
temp=cp_data(:,1); %Collecting Temperature Data from Data File.
cp=cp_data(:,2); %Collecting CP Data from Data File.
for d=1:10 %Using FOR loop to create Predicted Curve at different polynomial degree.
[coeff,S,mu] = polyfit(temp,cp,d); %in build "polyfit()" command is used to find coefficients for Predicted Curve.
Predicted_Cp=polyval(coeff,temp,S,mu); %in build "polyval()" command is used to solve and collect CP Data for Predicted Curve.
% Calculation of Goodness of Fit
% 1.The sum of squares due to error(SSE).
for i=1:length(Predicted_Cp); %Using FOR loop to calculate errors at every value for Predicted Curve.
sse(i)=(cp(i)-Predicted_Cp(i))^2; %Calculating errors square at every value for Predicted Curve.
end %Ending 'for' function.
SSE(d)=sum(sse); %Sumation of errors of each value of Predicted Curve.
% 2.R-Square.
for i=1:length(Predicted_Cp); %Using FOR loop to calculate errors at every value for Predicted Curve.
ssr(i)=(Predicted_Cp(i)-(sum(cp)/length(cp)))^2; %Calculating SSR at every value for Predicted Curve.
end %Ending 'for' function.
SSR(d)=sum(ssr); %Sumation of SSR of each value of Predicted Curve.
SST(d)=SSE(d)+SSR(d); %Calculating SST of Predicted Curve.
Rsq(d)=SSR(d)/SST(d); %Calculating R-Square of Predicted Curve.
% 3.Adjusted R-Square.
k=length(coeff)-1; %Calculating independent variables in Predicted Curve.
Rsq_adj(d)=1-[(1-Rsq(d)^2).*(length(cp)-1)/(length(cp)-k-1)]; %Calculating Adjusted_R-Square value of Predicted Curve.
% 4.Root mean square error(RMSE).
RMSE(d)=(SSE(d)/length(cp))^(0.5); %Calculating RMSE value of Predicted Curve.
% Plotting the CURVES
plot(temp,cp,'color','g','linewidth',6) %Ploting Original Data Curve.
hold on %Command to add multiple Plots in a single Figure.
plot(temp,Predicted_Cp,'color','r','linewidth',3) %Ploting Predicted Curve.
txt1=sprintf('Degree of Polynomial is %1.0f',d);%Text to display degree of polynomial of Predicted Curve on plot.
txt2='The Goodness of Fit'; %Text to display on the plot.
txt3=sprintf('SSE %1.4f',SSE(d)); %Text to display SSE of Predicted Curve on plot.
txt4=sprintf('R^2 %1.4f',Rsq(d)); %Text to display R^2 of Predicted Curve on plot.
txt5=sprintf('Adjusted R^2 %1.4f',Rsq_adj(d)); %Text to display Adujsted_R^2 of Predicted Curve on plot.
txt6=sprintf('RMSE %1.4f',RMSE(d)); %Text to display RMSE of Predicted Curve on plot.
txt={txt1,txt2,txt3 txt4,txt5,txt6}; %Text to display Goodness of Fit of Predicted Curve on plot.
text(2000,1000,txt,'HorizontalAlignment','center'); %Postion & Text to display Goodness of Fit of Predicted Curve on plot.
hold off %Command to stop adding multiple Plots in a single Figure.
xlabel('Temperature [K]') %Labelling X-Axis.
ylabel('Specific Heat (Cp) [KJ/(kg*K)') %Labelling Y-Axis.
legend('Orignal Curve','Predicted Curve','location','northwest') %Adding Legends on Plot.
M(d)=getframe(gcf); %Convert the Plot Figure into movie frame.
pause(3); %Pause time between the two consecutive Plot Figures.
end %Ending 'for' function.
movie(M) %Function used to make a movie/animation from movie frames.
videofile=VideoWriter('Best_Curve_Fit_by_Poly_Degree.avi','Uncompressed AVI'); %Creating Video file name and profile of it.
open(videofile) %Opening the video file.
writeVideo(videofile,M) %Writing in the video file with collected movie frames.
close(videofile) %Closing the video file.
Explanation/Workflow for Best Curve Fit by Poly Degree
- Here the code is the same as the Performing_Curve_Fitting.m code, there are only two changes here
- Change in the polyfit() and polyval() commands.
- For centering and scaling syntax for the ‘polyfit()’ command is,
- Here also returns mu, which is a two-element vector with centering and scaling values, mu(1) is mean(x), and mu(2) is std(x). Using these values, polyfit centers x at zero and scales it to have a standard deviation as 1.
- Here in the above code ‘polyfit()' command is entered as the above syntax which will calculate the values of ‘mu' and the value 'S’ along with the coefficients of the polynomial.
- Then values of ‘mu’ and 'S’ are given as inputs along with temperature values for the ‘polyval()’ command to evaluate the polynomial
- Now when we run the program, the warning found before will not come this time, because centering and scaling transformation improves the numerical properties of both the polynomial and the fitting algorithm.
- But when we increase the order of polynomial some phenomena will occur if we keep on increasing the order of the polynomial, this phenomenon is called as Overfitting of the curve.
- Overfitting a model is a condition where a statistical model begins to describe the random error in the data rather than the relationships between variables.
- This problem occurs when the model is too complex.
- Overfit regression models have too many terms for the number of observations. When this occurs, the regression coefficients represent the noise rather than the genuine relationships in the data.
- The extrapolation done by this over fitted will produce very low accurate results due to higher-order terms and due to many terms and the R square value thus obtained will be misleading as this polynomial will satisfy only the current data points and cannot predict the value for the next points as the next point will be downwards, but the actual trend is increasing in nature.
- So first we have to find the correct polynomial curve fit and then only we have to apply to center and scaling if needed to avoid the warning.
- But using centering and squaring is not always preferred instead, a split-wise method is used to avoid the warnings.
- For centering and scaling syntax for the ‘polyfit()’ command is,
- FOR loop is used to increase the degree of polynomial from 1:10 to observe the Goodness of Fit of Predicted Curve with increasing in the degree of the polynomial.
- Here in polyfit(x,y,n) command “n” (degree of polynomial) changes/increment with using FOR loop
- From the above observations, we can see that by increasing the order of polynomial we are getting better results.
- After getting the results of the plots of variation with an increase in Degree of Polynomial.
- After getting every curve fit from the results, and by collecting every plot with different Degree of Polynomial we create the animation movie of the predicted curve by increasing its degree of the polynomial.
- Step-Wise Explanation is provided in the code by using next to its comments.
- The split-wise method also gives more goodness of curve for the same polynomial order.
- Change in the polyfit() and polyval() commands.
- Results
- Performing Best Curve Fit by Using Curve Split-Wise Program is attached below.
- File Name : Best_Curve_Fit_by_Splitting.m
%OBJECTIVES OF THE PROJECT:
%Write code to fit a linear and cubic polynomial for the Cp data.
%Plot the linear and cubic fit curves along with the raw data points. Title and axes labels are a must, legends could be shown if necessary.
%Write a code to show the split-wise method.
%Explain the parameters used to measure the fitness characteristics for both curves.
close all
clear all
clc
cp_data =load('data'); %Loading the Data File.
temp=cp_data(:,1); %Collecting Temperature Data from Data File.
cp=cp_data(:,2); %Collecting CP Data from Data File.
for d=[1,3]%Using FOR loop to create Predicted Curve at Linear & Cubic degree.
for s=1:10; %Using FOR loop to Split the curve at Different Quantity.
a=floor(linspace(1,3200,s+1)); %Splitting the curve in equal Amount.
%floor(X) rounds each element of X to the nearest integer less than or equal to that element.
for i=1:length(a)-1 %Using FOR loop to create Predicted Curve at Different Splitted Sections.
b=a(:,i); %Collecting Starting point of Section.
c=a(:,i+1); %Collecting Ending point of Section.
temp_i=temp(b:c); %Collecting Temperature data for/of a Section.
cp_i=cp(b:c); %Collecting CP data for/of a Section.
[coeff_i,S,mu] = polyfit(temp_i,cp_i,d); %in build "polyfit()" command is used to find coefficients for Predicted Curve.
Predicted_Cp(b:c)=polyval(coeff_i,temp_i,S,mu); %in build "polyval()" command is used to solve and collect CP Data for Predicted Curve.
end
% Calculation of Goodness of Fit
% 1.The sum of squares due to error(SSE).
for i=1:length(Predicted_Cp); %Using FOR loop to calculate errors at every value for Predicted Curve.
sse(i)=(cp(i)-Predicted_Cp(i))^2; %Calculating error square at every value for Predicted Curve.
end %Ending 'for' function.
SSE(s)=sum(sse); %Sumation of errors of each value of Predicted Curve.
% 2.R-Square.
for i=1:length(Predicted_Cp); %Using FOR loop to calculate errors at every value for Predicted Curve.
ssr(i)=(Predicted_Cp(i)-(sum(cp)/length(cp)))^2; %Calculating SSR at every value for Predicted Curve.
end %Ending 'for' function.
SSR(s)=sum(ssr); %Sumation of SSR of each value of Predicted Curve.
SST(s)=SSE(s)+SSR(s); %Calculating SST of Predicted Curve.
Rsq(s)=SSR(s)/SST(s); %Calculating R-Square of Predicted Curve.
% 3.Adjusted R-Square.
k=length(coeff_i)-1; %Calculating independent variables in Predicted Curve.
Rsq_adj(s)=1-[(1-Rsq(s)^2).*(length(cp)-1)/(length(cp)-k-1)]; %Calculating Adjusted_R-Square value of Predicted Curve.
% 4.Root mean square error(RMSE).
RMSE(s)=(SSE(s)/length(cp))^(0.5); %Calculating RMSE value of Predicted Curve.
%Plotting the Surves
plot(temp,cp,'color','g','linewidth',6) %Ploting orignal Data Curve.
hold on %Command to add multiple Plots in a single Figure.
plot(temp,Predicted_Cp,'color','r','linewidth',3) %Ploting Predicted Curve.
plot(temp(a),Predicted_Cp(a),'o','markersize',3,'markerfacecolor',[0 0 0 ]) %Marking start point of Predicted Curves.
txt1=sprintf('Splitting curve into %1.0f equal sections',s);%Text to display no. of sections(split) of Predicted Curve on plot.
txt2=sprintf('Degree of Polynomial is %1.0f',d); %Text to display on plot.
txt3='The Goodness of Fit'; %Text to display the degree of the polynomial of Predicted Curve on the plot.
txt4=sprintf('SSE %1.4f',SSE(s)); %Text to display SSE of Predicted Curve on plot.
txt5=sprintf('R^2 %1.4f',Rsq(s)); %Text to display R^2 of Predicted Curve on plot.
txt6=sprintf('Adjusted R^2 %1.4f',Rsq_adj(s)); %Text to display Adjusted_R^2 of Predicted Curve on plot.
txt7=sprintf('RMSE %1.4f',RMSE(s)); %Text to display RMSE of Predicted Curve on plot.
txt={txt1,txt2,txt3,txt4,txt5,txt6,txt7}; %Text to display Goodness of Fit of Predicted Curve on plot.
text(2000,1000,txt,'HorizontalAlignment','center'); %Postion & Text to display Goodness of Fit of Predicted Curve on plot.
hold off %Command to stop adding multiple Plots in a single Figure.
xlabel('Temperature [K]') %Labelling X-Axis.
ylabel('Specific Heat (Cp) [KJ/(kg*K)') %Labelling Y-Axis.
legend('Orignal Curve','Predicted Curve','location','northwest') %Adding Legends on Plot.
if d==1; %Using if function to collect Plot figures of Linear Predicted Curve
M1(s)=getframe(gcf); %Convert the Plot Figure into movie frame.
pause(1); %Pause time between the two consecutive Plot Figures.
elseif d==3; %Using elseif function to collect Plot figures of Cubic Predicted Curve
M3(s)=getframe(gcf); %Convert the Plot Figure into movie frame.
pause(1); %Pause time between the two consecutive Plot Figures.
end %Ending 'if' function.
end %Ending 'for' function.
end %Ending 'for' function.
movie(M1) %Function used to make a movie/animation from movie frames.
videofile=VideoWriter('Best_Linear_Curve_Fit_by_Splitting.avi','Uncompressed AVI'); %Creating Video file name and profile of it.
open(videofile) %Opening the video file.
writeVideo(videofile,M1) %Writing in the video file with collected movie frames.
close(videofile) %Closing the video file.
movie(M3) %Function used to make a movie/animation from movie frames.
videofile=VideoWriter('Best_Cubic_Curve_Fit_by_Splitting.avi','Uncompressed AVI'); %Creating Video file name and profile of it.
open(videofile) %Opening the video file.
writeVideo(videofile,M3) %Writing in the video file with collected movie frames.
close(videofile) %Closing the video file.
Explanation/Workflow for Best Curve Fit by Splitting
- Here the code is Similar to the Best_Curve_Fit_by_Poly_Degree.m code, there are only some changes here.
- FOR loop(1st)-{d=[1,3]} is used to perform the Split-Wise Curve Fitting for both
- Linear Polynomial (1st Degree curve)
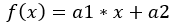
- Cubic Polynomial (3rd Degree curve)
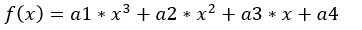
- Linear Polynomial (1st Degree curve)
- FOR loop(2nd)-{s=1:10} is used to split the data into 1:10 sections to observe the Goodness of Fit of Predicted Curve with increasing in sections of split data. [FOR loop(2nd) is used inside FOR loop(1st)]
- Here code “a=floor(linspace(1,3200,d+1));” is used in the FOR loop to split the data with incrementing in sections to observe the effect on Goodness of Fit of the Predicted curve.
- “linspace(x1,x2,n)” command is used to generate a linearly spaced vector. The spacing between the points is (x2-x1)/(n-1).
- After splitting the curve into equal sections, sometimes sections were in fractional type, and data can not get divided into fraction values, so the “floor(x)” command is used.
- “floor(x)” command rounds each element of X to the nearest integer less than or equal to that element.
- Here code “a=floor(linspace(1,3200,d+1));” is used in the FOR loop to split the data with incrementing in sections to observe the effect on Goodness of Fit of the Predicted curve.
- FOR loop(3rd)-{i=length(a)-1} is used to perform the Curve Fitting section wise for given data.[FOR loop(3rd) is used inside FOR loop(2nd)]
- Here code “b=a(:,i);” is used to collect Starting point of the Section.
- Here code “c=a(:,i+1);” is used to collect Ending point of Section.
- Here code “temp_i=temp(b:c);” is used to collecting Temperature data for/of a section.
- Here code “cp_i=cp(b:c);” is used to collecting CP data for/of a Section.
- Now “ployfit” and “polyval” commands are used for the curve fitting of the created section.
- A combined curve fit of each and every section is created and stored in “Predicted_Cp”.
- FOR loop(1st)-{d=[1,3]} is used to perform the Split-Wise Curve Fitting for both
- We calculate the goodness parameters SSE, R-Square, Adjusted R-Square, and RMSE for the curves fit and display the parameters on the plot.
- The graph is plotted for the original and predicted values.
- From the above observations, we can see that by increasing the Split sections we are getting better results.
- After getting the results of the plots of variation with an increase in split sections.
- After getting every curve fit from the results, and by collecting every plot is split with different quantity of sections we create the animation movie of the predicted curve by increasing its sections.
- IF-{if d==1;} & ELSEIF-{elseif d==3;} function is used to create the separate animation for Split-Wise Curve Fitting for both
- Linear Polynomial (1st Degree curve)
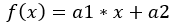
- Cubic Polynomial (3rd Degree curve)
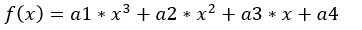
- Linear Polynomial (1st Degree curve)
- Step-Wise Explanation is provided in the code by using next to its comments.
- IF-{if d==1;} & ELSEIF-{elseif d==3;} function is used to create the separate animation for Split-Wise Curve Fitting for both
- Errors faced while running the Best_Curve_Fit_by_Poly_Degree.m Program
- Array indices must be positive integers or logical values.
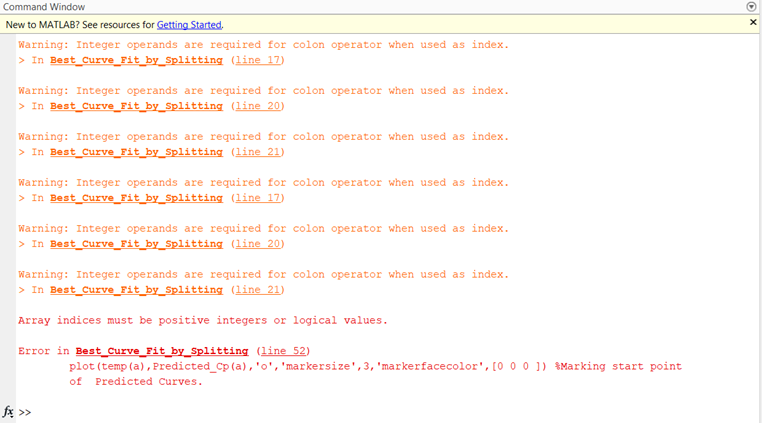
- To get rid of the error I looked upon the internet regarding the error and found that using the “floor(x)” function the error can be eliminated.
- “floor(x)” command rounds each element of X to the nearest integer less than or equal to that element.
- Hence now all the Array indices become positive integers or logical values.
- Results
5.CONCLUSION:
- Thus, a code to fit a linear and cubic polynomial for the Cp data is executed successfully to specific heat data provided using MATLAB.
- Goodness parameters for each curve are evaluated and are compared with the results using the MATLAB toolbox.
- A similar approach can be used for other curve fits to predict any kind of data.
- Using the split-wise method will give more goodness to the curve.
6.REFERENCES:
Leave a comment
Thanks for choosing to leave a comment. Please keep in mind that all the comments are moderated as per our comment policy, and your email will not be published for privacy reasons. Please leave a personal & meaningful conversation.
Other comments...
Be the first to add a comment
Read more Projects by Amit Chilap (11)
Week-3 Challenge: ADVISOR Tool
Introduction to HEV using MATLAB & Simulink Week-3 Challenge: ADVISOR Tool AIM: To simulate the given data and conditions for an EV using Advisor Tool in MATLAB. About ADVISOR ADVISOR, NREL’s Advanced Vehicle Simulator, is a set of model, data, and script text files for use with MATLAB and Simulink. It…
04 Jul 2022 11:04 AM IST
Project -BAJA All Terrain Vehicle (ATV) model
Simulink for Mechanical & Electrical Engineers - Challenges Final Project Aim To study, analyze and make a detailed report on BAJA All Terrain Vehicle (ATV) model using Simulink & compare between its different modes. Objective Prepare a technical report explaining the model properties & comments on the results.…
03 Jun 2021 03:25 AM IST
Week - 4
Simulink for Mechanical & Electrical Engineers Challenges = Week 4 Aim To Make a Simulink model using State-Flow for given questions. Questions & Solution Q1. Implement control logic of a “washing machine” using Stateflow as per given sequence: If the power supply is available, the system gets activated. If the Water supply…
21 May 2021 06:29 PM IST
Week -2
Simulink for Mechanical & Electrical Engineers Challenges = Week 2 Aim To Make a Simulink model of Doorbell using solenoid block. To Use a thermistor to sense the temperature of a heater & turn on or turn off the fan according to temperature. Questions & Solution Q1. Make a Simulink model of Doorbell using…
14 May 2021 12:30 AM IST
Related Courses




Skill-Lync offers industry relevant advanced engineering courses for engineering students by partnering with industry experts.
Our Company
4th Floor, BLOCK-B, Velachery - Tambaram Main Rd, Ram Nagar South, Madipakkam, Chennai, Tamil Nadu 600042.
Top Individual Courses
Top PG Programs
Skill-Lync Plus
Trending Blogs
© 2025 Skill-Lync Inc. All Rights Reserved.












