Constrained Optimisation Using Lagrange Multipliers

Problem:

Minimize: `5-(x-2)^2 -2(y-1)^2`;

subject to the following constraint: `x + 4y = 3`

1) Lagrange Multipliers

Lagrange multipliers technique is a fundamental technique to solve problems involving constrained problems. This method is utilised to find the local minima and maxima subjected to (at least one) equality constraints.

The fundamental concept in a constrained optimisation problem is to maximise or minimise a certain equation but keeping some other constraint equation in consideration as well. The equation which is to be optimised is called the objective function. For example, if a company has to maximise its revenue, it may say that they have a model (some mathematical equation) for the revenue `f(x,y)`, where, say, x and y are the material cost and labour hours respectively. The company can input more and more x and y to increase the revenue. But the company has a certain constraint for its budget. And say that the model for their budget is given by the function ` g(x,y)`. In this situation, the company wants to maximise its revenue given the budget. When optimised, we get the values for x and y that will maximise the revenue within the given budget.

In order to solve the problem, we use a Lagrangian form:

`grad L(x,y,lambda): grad(f(x,y) - lambda ( c(x,y) - k)`

where `f(x,y)` is the objective function, `c(x,y) = k` is the constrained equality and `lambda` is known as the Lagrange multiplier(s). We solve for `grad L(x,y,lambda) = 0` and find the values of x and y.

1.1 Geometrical Interpretation:

Considering our problem, we have:

Objective function, `f(x,y) : 5-(x-2)^2 -2(y-1)^2`

Constraint, `c(x,y) : x + 4y = 3`

Now looking at the objective function, what 'f(x,y)' actually is that in the x-y plane, `5-(x-2)^2 -2(y-1)^2 =` constant is the collection of all points (x,y) where it equates to the 'constant' value. Now, this constant can have different values. If we equate `f(x,y)` to z, the values of x and y in the objective function can be determined by fixing all the possible values for z and calculating the (x,y) values which may be real only, or complex. A 3D plot of the objective function can be obtained in MatLab as shown in the code below:

%Plotting the objective function in 3D using MATLAB

%Symbolic
 
syms x y z                %syms command allows the creation of  symbolic variables. 

z = 5-(x-2)^2 -2*(y-1)^2; %the objective function. 

fsurf(x,y,z)              % plots a 3D plot (surface)

title('Plot of Objective Function')
xlabel('X')
ylabel('Y')
zlabel('Z')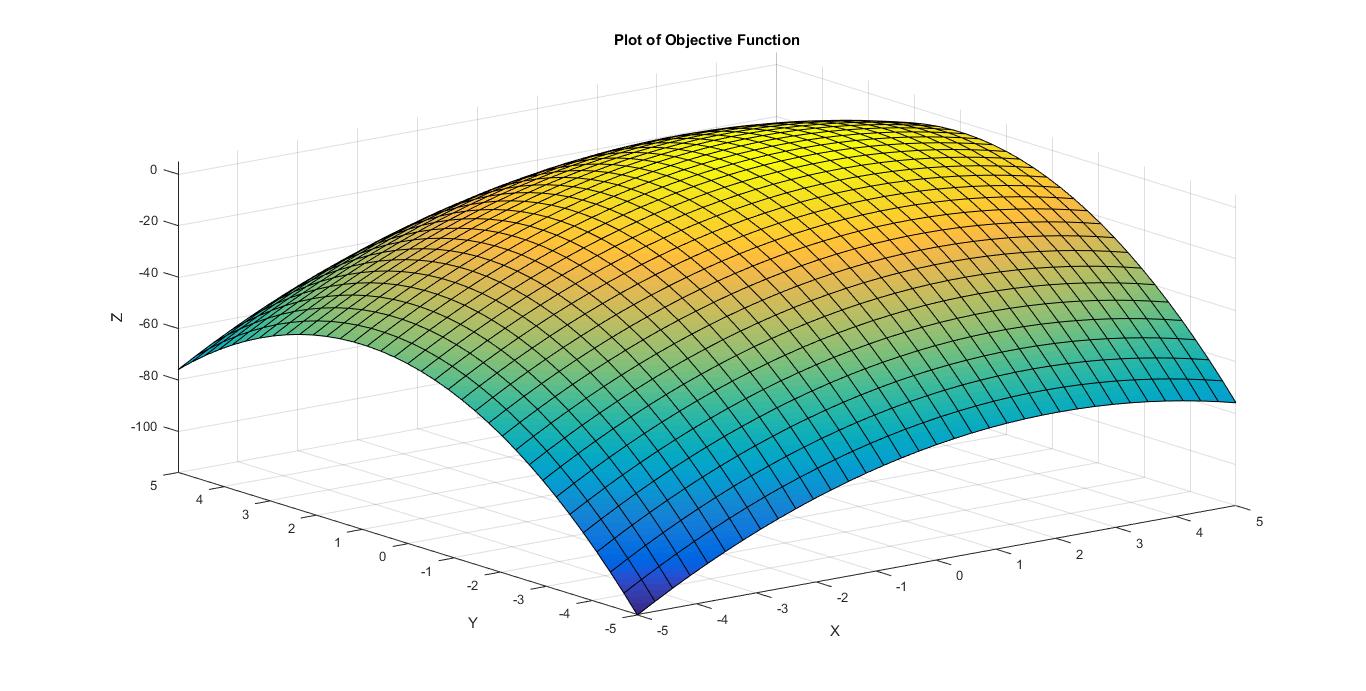

Fig. 1: 3D, Surface Plot of the Objective Function.

Clealy, the curve has only global maxima and no minima i.e., the curve keeps on going in the negative z-direction, but halts somewhere (has a maximum) in the positive z-direction. To calculate it, we can simply differentiate the function with respect to x and y and then equate each differential to zero.

`[[partial/(partialx) f(x,y)], [partial/(partialx) f(x,y)]] = [[0],[0]]` {scalar matrix}

`[[partial/(partialx) (5-(x-2)^2 -2*(y-1)^2)], [partial/(partialy) (5-(x-2)^2 -2*(y-1)^2)]] = [[0],[0]]`

`[[-2(x-2)],[-4(y-1)]] = [[0],[0]]`

Solving, `-2(x-2) = 0` and `-4(y-1) = 0`, we have, `(x,y) = (2,1)`. Putting this value of (x,y) in the objective function, we get: `f(2,1) = 5 - (2-2)^2 - 2(y-1)^2 = 5`. Thus, the function has a global maxima, 5 at (2,1) and no global minima.

1.1.a MatLab Code For Maxima:

%Finding the Maximum of the Objective function

syms x y z

z = 5-(x-2)^2 -2*(y-1)^2;

deriv = [diff(z,x),diff(z,y)]; %diff(z,x) differentiates z w.r.t x.

x_y = [solve(deriv(1) == sym(0),x),solve(deriv(2) == sym(0),y)];
%x_y contains the symbolic values of x and y at the extrema

x1 = double(x_y(1));    %converts the first element, x value to a number
y1 = double(x_y(2));

z_max = 5-(x1-2)^2 -2*(y1-1)^2; %calculates the value of the function at x_y

D = sprintf('The function has a maximum of %d at (x,y) = (%d,%d)',z_max,x1,y1);
disp(D)


>>>
The function has a maximum of 5 at (x,y) = (2,1)

1.1.b Plotting Objective Function and Constraint

Now, to optimise the above function, we have to look for the constraint. Here, our constraint is a line in the x-y plane. If we draw a line with the objective function, we get a plot like the one shown in Fig. 2.

%Plotting Objective Function and Constaint Function in MATLAB


syms x,y,z

z = 5-(x-2)^2 -2*(y-1)^2;
fsurf(x,y,z,'EdgeColor','None') %creates a smooth interpolated coloured surface

title('Plot of Objective and Constrain Functions')
xlabel('X')
ylabel('Y')
zlabel('Z')

hold on                  %keeps the previous plot on the graph

y = (3- x)/4             %constraint

fplot(y,'linewidth',2)   %plots the symbolic thicker planar curve

     

Fig. 2: Objective Function and Constraint Plot.

1.1.c Contours

Our solution lies where the constraint line and the objective function meet. In other words, the minimum of the objective function which is on the graph of the constraint, is the solution. To have a better visualisation of the two curves meeting, we must see both the plots in a single plane. As the constraint equation is solely in the X-Y plane (z=0), we need to project the objective function onto the X-Y plane. The curves obtained are called contours. A contour is a set of lines (curves) of a function of two variables along which the function has a constant value (z in our case). The contour of the objective function can be obtained in MatLab with the help of the following code:

%Plotting Contours of the Objective Function and the Constraint Line


syms x y z
z = 5-(x-2)^2 -2*(y-1)^2;  %objective funstion

fc = fcontour(z,'r');  %fcontour() is the contour function and fc stores its handle

fc.LevelList = [-40 -30 -20 -10 5 0 1  3 4 4.5 4.9 10 20 30 40];
%LevelList is the method of fcontour which specifies the values of the function and generate curves. Eg., in our case, it will assign z values of -40,-30,-20....40 and draw the contour lines at these values of the function.

axis([-4 4 -4 4])   %fixes the axis
hold on
y = (3-x)/4;        %constraint

fplot(y,'b')        %plot as a blue line
grid on
title('Contour of the Objective Function and the Constraint Line')
xlabel('X')
ylabel('Y')
legend('Contour','Constraint Line')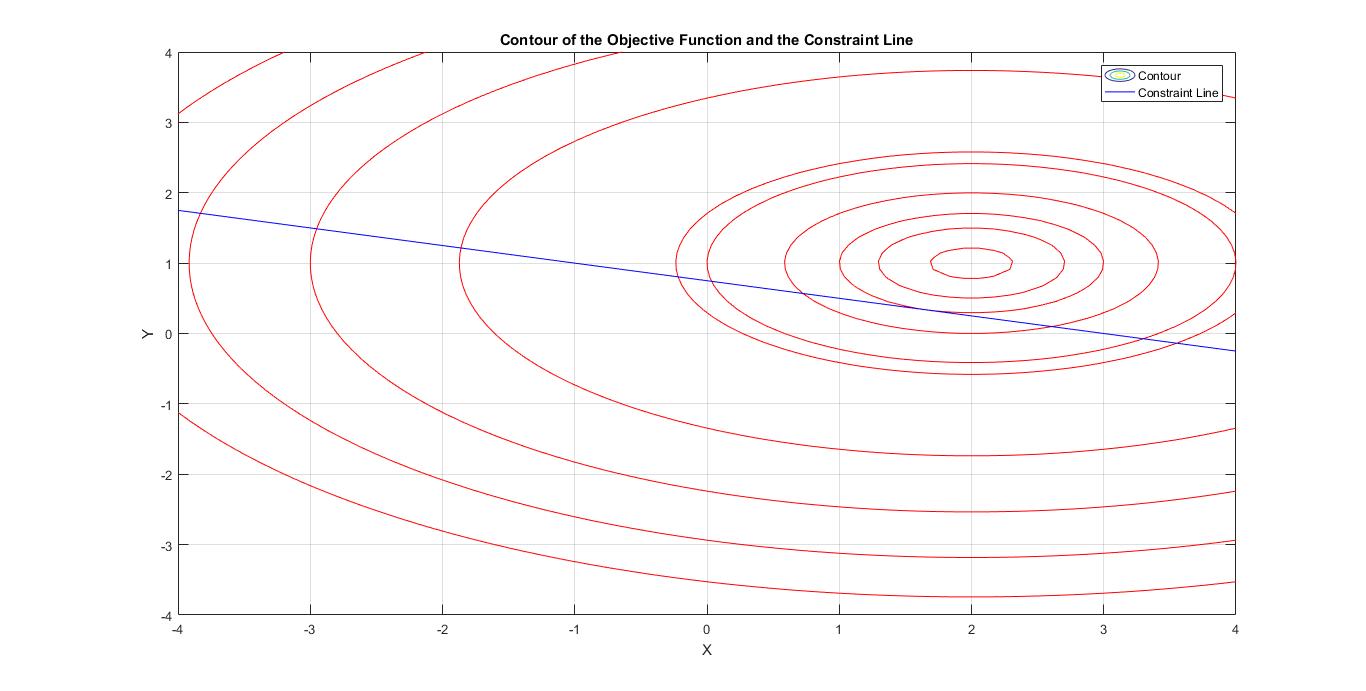

Fig. 3: Contour of the Objective Function and the Constrained Line

From the fig. 3, it is quite clear now that each constant value of the `f(x,y)` yields different contour curves. We know that the function has a maxima at (2,1) where the contour is just a point on the x-y plane. Now, as we move away from this point in the x-y plane, the function will tend to become more and more negative up to (-)infinity. However, our constraint puts a limit to this. We only want to find the minimum of the curve where the constraint is also true. That is, (x,y) must be satisfied both by the objective function as well as the constraint. This means we have to find the contour curve which as much far away from the maximum but at the same time not more away than the constraint line. In simple terms, the constraint line is tangent to the contour curve at the optimisation level.

We know that the gradient of a function at a point gives a vector that is normal to the curve. Mathematically,

`grad f(x,y) = [[partial/(partialx) f(x,y)],[ partial/(partialy) f(x,y)]]` {a vector}

1.1.d Tangency

As the constraint line is tangent to the curve, a normal at the point of tangency will be normal to both constraint line and the contour i.e., gradients of either function will be proportional to each other. Fig. 4 shows the idea visually.

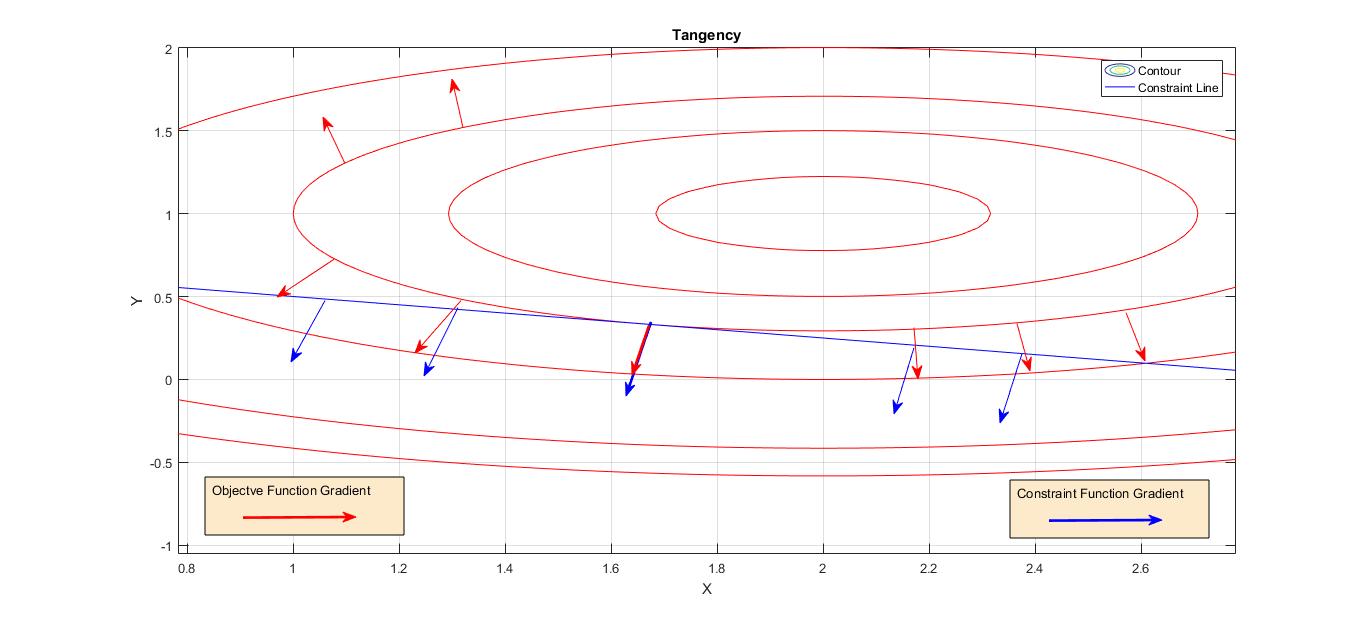Fig. 4: Tangency, Gradients of the Objective and Constraint

Mathematically,

`grad f(x,y) prop grad c(x,y)`

or, `grad f(x,y) = lamda grad c(x,y)`

where `lambda` is the proportionality constant.

`[[partial/(partialx) f(x,y)], [partial/(partialy) f(x,y)]] = lambda [[partial/(partialx) c(x,y)], [partial/(partialy) c(x,y)]]`

Solving the above equation gives us two two equations and three variables, add the constriant equation, and we have three variables and three equations. Using this we can easily calculate the value of (x,y) and ultimately `f(x,y)_(min)`.

`[[partial/(partialx) (5-(x-2)^2 -2*(y-1)^2)], [partial/(partialy) (5-(x-2)^2 -2*(y-1)^2)]] = lambda [[partial/(partialx) (x + 4y)], [partial/(partialy) (x + 4y)]]`

`[[-2(x-2) ], [-4(y-1)]] = lambda [[ 1],[4]]`

which gives: `-2(x-2) = lambda` and `-4(y-1) = 4lambda`

Eliminating `lambda`, we have:

`-2(x-2) = -(y-1) => y = 2x -3`

Substituting the value of y in the constraint equation, we have:

`x + 4(2x-3) = 3 => 9x - 12 = 3 => x= 15/9 = 5/3`

`therefore y = 2(5/3) - 3 = 10/3 - 3= 1/3`

Thus, `f(x,y)_(c min ) = f(5/3,1/3) = 5 - (5/3 -2)^2 - 2(1/3-1)^2 = 4`

The value of `lambda` (which is calculated if one want's to check the proportionality) can also be calculated.

we have, `-4(y-1) = 4 lambda => lambda = -(1/3-1) = 2/3`

This implies that the gradient or normal of the objective function is 2/3 times the gradient of the constraint line at (5/3,1/3), and they are in the same direction.

1.2 Lagrangian Form:

To put all the equations in a beautiful matrix form, Lagrange Multipliers equation can be put in a single gradiant equation form. If the constraint function is `c(x,y) = k`, where `k` is some constant, putting `g(x,y) = c(x,y)-k = 0`, we have:

`grad f(x,y) = lamda grad c(x,y) = lambda grad g(x,y)`

or, `grad f(x,y) - lamda grad g(x,y) = 0 => grad(f(x,y) - lambda g(x,y) = 0 `

`therefore grad L(x,y,lambda): grad(f(x,y) - lambda (g(x,y))=0`

Which gives all the required equations in a single matrix form.

Inserting the equations of the problems we have,

`grad L(x,y,lambda) = grad( 5-(x-2)^2 -2*(y-1)^2 - lambda ( x+4y -3))`

`[[partial/(partialx) (5-(x-2)^2 -2*(y-1)^2 - lambda ( x+4y -3))], [partial/(partialy) (5-(x-2)^2 -2*(y-1)^2 - lambda ( x+4y -3))], [partial/(partial lambda) (5-(x-2)^2 -2*(y-1)^2 - lambda ( x+4y -3))]] = [[0],[0],[0]]`

Which gives back the three equations we required to solve for the constrained minimisation. Note that the third row in the below matrix is the constraint equation in `g(x,y) = 0` form.

`[[- 2(x-2) - lambda], [ -4(y-1) - 4 lambda], [-x-4y + 3]] = [[0],[0],[0]]`

`[[- 2(x-2) - lambda], [ -4(y-1) - 4 lambda], [x+4y - 3]] = [[0],[0],[0]]`

Note: The LaGrange multiplier equation can also be written in the form:

`therefore grad L(x,y,lambda): grad(f(x,y) + lambda (g(x,y))=0`

In this case, the sign of `lambda` is opposite to that of the one obtained from the previous equation. For example, if we calculate the Lagrange multiplier for our problem using this formula, we get `lambda = - 2/3`. However, `x` and `y` remain unchanged. Also, the gradient of the objective function will still be `2/3` times that of the constraint at `(5/3,1/3)`.

1.3 MatLab Code To Solve Lagrangian

Using, Matlab's 'diff()' command to differentiate a function, 'solve()' command to solve an equation or set of linear equations, we can write a code to solve the steps involved in manual calculation to solve for `f(x,y)_(c min)` and `lambda`.

Code:

%Optimsing the Objective Function Using the Lagrange multipliers


%1) Define symbolic functions

syms x y z t l
clc
z = 5 - (x-2)^2 - 2*(y-1)^2; %objective function
t = x + 4*y - 3;              %constraint

%2) Obtain gradients

%2.1) gradiant of the objective function
deriv_O = [diff(z,x),diff(z,y)];   %diff(z,x) differentiates z w.r.t x.

%2.2) gradiant of the constraint
deriv_C = [diff(t,x),diff(t,y)]; %diff(z,x) differentiates z w.r.t x.

%3) Putting the gradients in the LaGrange form

M = deriv_O + l*deriv_C; %deriv_O - deriv_C would result in opp. sign of lambda
%Here, the matrix addition is done element-wise. 

%4) Solving the equations

sol = solve([M(1),M(2),t],[x,y,l]); %three equations, variables
%sol is a struct containing the values of symbolic x,y and l.

values = [string(sol.x),string(sol.y),string(sol.l)]; %convertind struct to strings

%5) Calculating the value of the function at optimimum values

f_opt = 5 - (double(sol.x)-2)^2 - 2*(double(sol.y)-1)^2; %converting symbolic valus to double precision numbers

%)6 Displaying the functions and results

E = sprintf(['For the constrained Optimisation problem: \n '...
    'objective function: \t%s \n Subjected to the cosntraint: \t%s'... 
    '\n\n x = %s, y = %s and lambda = %s \n Where the value of the '...
    'objective function is = %d'],z,t,values,f_opt);
disp(E)

%if M = derivO - derivC is used, lamda would be 2/3



>>>
For the constrained Optimisation problem: 
 objective function: 	5 - 2*(y - 1)^2 - (x - 2)^2 
 Subjected to the cosntraint: 	x + 4*y - 3

 x = 5/3, y = 1/3 and lambda = -2/3 
 Where the value of the objective function is = 4

NOTE: Constraint optimisation can be solved in both Python as well as Matlab. In Python, the 'scipy.optimize' library has the essential functions to solve constrained optimisation problems. In Matlab, constrained optimisation problems can be solved by various functions like 'fmincon', 'fseminf' and 'fminbnd'. One can also utilise the Optimisation Toolbox for an interactive optimisation. However, most of these programs require initial guesswork. The initial value must be as close to the solution as possible, which can often be challenging. Another problem with these functions is that they may get stuck in local minima instead of the global minima. One needs to set proper inputs to these functions in order to get the best results. Optimisation techniques like the Genetic Algorithm become essential in such situations. For the working of Genetic Algorithm optimisation in Matlab, check out Genetic Algorithm. Finding The Global Maxima of The Stalagmite Function in MatLab. [https://bit.ly/2CbQmox]

***END***