Solving second order ODEs

1.AIM:

To write a program that solves the following ODE.

This ODE represents the equation of motion of a simple pendulum with damping.

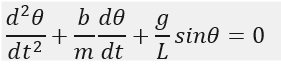
2.GOVERNING EQUATIONS IF ANY:

• The main function used in this program is “ode45”, its information is provided below.

Ode45 is a function in MATLAB that solves ordinary or partial differential equations using a numerical method. The numerical method in question here is the 4th order Runge Kutta method.

Before looking at the syntax and the function, let us understand what we mean by solving an ode and the Runge-Kutta method.

To solve an ODE, we have to integrate and solve for the variable. Assuming we have an ode du, we would solve for u by integrating du provided some limits of integration. However, rather than direct integration, we can use a numerical solver, by discretizing the equation, that is, we convert the ODE into a linear equation and then solve this equation to approximate the solution.

For our purpose, we will be looking at the Runge-Kutta method, which is a first order ODE solver for initial value problems. That is, provided an initial condition, we will be able to use the 4th order RK method to solve the solution.

How the RK method works:

The RK method requires,

An initial condition (y0).

Step size (h).

Assuming we have a problem, y’ = f(t,y)

For the RK method, we need to define 4 terms,

where h is the step size or time step.

Using these terms, we use the relation provided below to solve for the solution at the next time step.

Let us take the example and take a look at an example.

From this we get y at the first time step, h=0.1 to be 1.1107. The value at the 2nd time step can be figured out using this value as a stepping point and we can step up to our end time.

How ode45 works:

The function ode45 takes 3 inputs. The 3 inputs are the function to be integrated, the time span, and the initial conditions.

The function would be one like shown in the above example. The time span would be the integration limits. This can be provided as a vector of 2 values, the initial and final time, or with a spacing using the linspace function. The solver will choose a step size that is most suitable for the solution to obtain a solution in the most optimal time possible. The initial condition would be the value of the function at t=0s.

The function can be provided in the form of an anonymous function,

[t,results] = ode45(@(x) x^2, tspan,y0)

Here, we are saying that we don’t know the value of x and that x is an input to the anonymous function that we have defined here. This is equivalent to defining a function that takes the input of x and gives the output of x^2.

The function can also be defined as a separate function. This function must take at least 2 inputs, which should be t and y, apart from other arguments, where t would be the current time and y would be the value of the function at the previous time step.

Assuming we have a function ode, the function must be defined as,

function [output] = ode(t,y,args)

where args refer to any other arguments that the function may take.

This function must then be input to ode45 as

[t,results] = ode45(@(t,y) ode(t,y,args), tspan, y0)

This is necessary to tell the function which arguments of the function are to be found by the solver.

As mentioned above, the RK method is a first order ODE solver and hence, so is ode45. Thus, any ODE to be integrated by ode45 must be provided as a set of first order ODEs.

3.OBJECTIVES OF THE PROJECT:

• The Objective is to write a program that solves the following ODE. This ODE represents the equation of motion of a simple pendulum with damping.

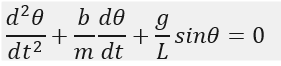
Given data:

L=1 metre,

m=1 kg,

b=0.05.

g=9.81 m/s2.

Simulate the motion between 0-20 sec, for angular displacement=0, angular velocity=3 rad/sec at time t=0.

• Following is the workflow of the program.
• We first convert the 2nd ODE into the 1st ODE.
• The conversation from 2nd ODE to 1st ODE is done in the supplementary program.
• We use the main inbuild function “ode45” to solve the 1st ODE.
• Ode45 using the RK method as mentioned above solve the 1st ODE and provides the results of the given equation.
• As in the results, the angular displacement and the angular velocity are calculated for each step value for a given time span.
• After getting the results then we plot the angular displacement and angular velocity vs time for a given time span.
• After getting every position of the pendulum from the results we plot its position for each time step.
• And by collecting every plot position of the pendulum we create the animation movie of the motion of the pendulum from the given initial conditions.

4.BODY OF THE CONTENT:

• MATLAB Programming language is used.
• Main Program is attached below.

• %Objective is to write a program that solves the following ODE. 
  %This ODE represents the equation of motion of a simple pendulum with damping.
  %(d^2(θ))/(dt^2 )+(b/m)*dθ/dt+(g/L)*sinθ=0.
  %Given data: L=1 metre, m=1 kg, b=0.05, g=9.81 m/s^2.
  %Simulate the motion between 0-20 sec, for angular displacement=0, angular velocity=3 rad/sec at time t=0.
   
  close all
  clear all
  clc
   
  b=0.05; %Damping Coefficient of Pendulum.
  g=9.81; %Gravitational Acceleration. In m/sec^2.
  l=1; %Length of Pendulum String. In m.
  m=1; %Mass of the Pendulum Bob. In kg.
   
  theta_0=[0;3]; %Initial Conditions of the Pendulum Position/Displacement and Velocity.
  t_span=linspace(0,20,500); %Time span of Pendulum Motion.
   
  [t,results]=ode45(@(t,theta) ode_func(t,theta,b,g,l,m),t_span,theta_0); %Solving the Differential Equation.
   
  figure(1) %Figure for plotting Displacement, Velocity VS Time.
  hold on %To add multiple Plots in single Figure.
  plot(t,results(:,1),'color','r') %Plotting Displacement VS Time.
  plot(t,results(:,2),'color','g') %Plotting Velocity VS Time.
  xlabel('TIME'); %Labelling X-Axis.
  ylabel('Displacement(Red) & Velocity(Green)') %Labelling Y-Axis.
  legend('Displacement','Velocity') %Displaying the Legends for Figure(1).
  title('Displacement, Velocity VS Time') %Providing Title to Figure(1).
   
  d=rad2deg(results(:,1))+180; %Converting Radians To Degree.
   
  %Making Animation for Pendulum Motion.
  ct=1;%Creating a string to record both Pendulum Positions.
  for i=1:length(d); %Using 'for' loop to collect every position of Pendulum.
  theta1=d(i); %Providing the angle to collect a position of Pendulum.
   
  %coordinates
  x0=0; %X-Coordinates of string attached to the Celling/Holder.
  y0=l+1; %Y-Coordinates of string attached to the Celling/Holder.
   
  x1 = l*sind(theta1); %X-Coordinates of string attached to the Pendulum Bob.
  y1 = 1+l+l*cosd(theta1); %Y-Coordinates of string attached to the Pendulum Bob.
   
   
  %Plotting
  figure(2) %Figure for plotting Motion of Pendulum.
  plot([x0 x1],[y0 y1],'linewidth',5) %Plotting of String.
  hold on %To add multiple Plots in single Figure.
  plot ([-y0/2 y0/2],[y0 y0],'linewidth',5) %Plotting of Celling/Holder of Pendulum.
  plot(x0,y0,'o','markersize',10,'markerfacecolor','[0 0 0 ]','markeredgecolor','r') %Plotting of Pendulum joint/hinge to Celling.
  plot(x1,y1,'o','markersize',25,'markerfacecolor','r','markeredgecolor','g') %Plotting of Pendulum Bob.
  hold off %Stopping addition of multiple Plots in single Figure.
  title('Motion of Damped Pendulum') %Providing Title to Figure(2).
  text(-1.8,2.75,'Pendulum bob is dropped from the 0 angular displacement &');
  text(-1.8,2.5,'at 3 rad/sec angular velocity with damping coefficient of 0.05.');
  text(-1.8,2.25,‘Given data: L=1 metre, m=1 kg, b=0.05, g=9.81 m/s^2');
   
  axis([-y0 y0 0 y0+1]) %Giving axis limits.
  if ct==1;
  pause(1) %Pause time for Displaying Initial Condition.
  else
  pause(0.002) %Pause time between the two consecutive positions of Pendulum.
  end
  M(ct) = getframe(gcf);%Convert the image of Pendulum Positions to movie frame.
  ct=ct+1; %Changing the string to record the next Pendulum Positions.
   
   
  end %Ending 'for' function.
   
   
  movie(M) %Function using the make a movie/animation from movie frames.
  v_p=VideoWriter('Motion_of_Damped_Pendulum.avi','Uncompressed AVI'); %Creating Video file name and profile of it.
  open(v_p) %Opening the video file.
  writeVideo(v_p,M) %Writing in the video file with collected movie frames.
  close(v_p) %Closing the video file.
  

• Supplementary Program for this program.

• %Supplementary programs:Function(ode_func) is to Solve ODE.
   
  function[dtheta_dt]=ode_func(t,theta,b,g,l,m)
   
  %Given Function/ODE is (d^2{theta}/d{t}^2)+(b/m)*(d{theta}/d{t})+(g/l)*sin(theta)=0
   
  %Simplifying to give ODE to solve.
  theta1=theta(1); %Collecting Angular Displacement.
  theta2=theta(2); %Collecting Angular Velocity.
  dtheta1_dt=theta2; %Relation between Angular Velocity & Angular Displacement.
  dtheta2_dt=-(b/m)*theta2-(g/l)*sin(theta1); %Simplified given
  dtheta_dt=[dtheta1_dt;dtheta2_dt]; %Output equation of function.
  end
  
  

• Step-Wise Explanation is provided above in the code.
• Since Checking the program at every step, No Error was found during programming.
• Therefore, no steps are taken to overcome Errors, & no Screenshots showing errors thrown in the command window

• Results
• 
• 

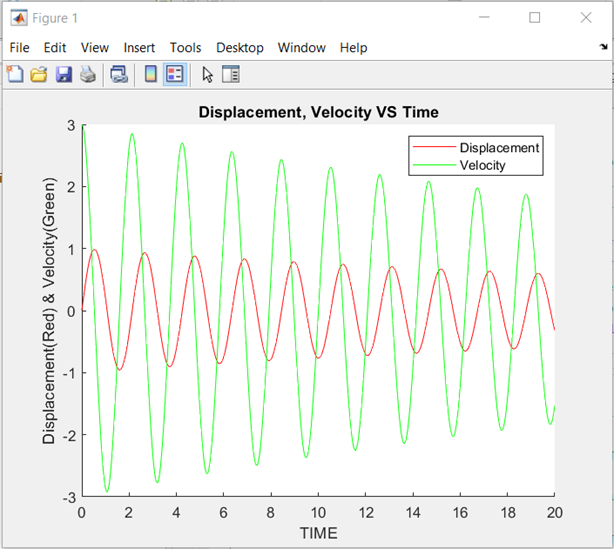
• I have also made a program with different initial conditions mentioned below.
• The pendulum bob is dropped from the pi/2 angular displacement & at 0 rad/sec angular velocity with a damping coefficient of 0.15(b=0.15) with Length = 4 metre, Mass = 2 kg, g=9.812 m/s².
• The output of that program is displayed below in the video.

5.CONCLUSION:

• Displacement & Velocity is reduced gradually, it directly depends upon the damping coefficient.
• Higher the damping coefficient faster the rate of reduction of Displacement and Velocity.
• Similarly, an increase in mass lowers the rate of reduction of Displacement and Velocity, & vice versa.
• The above conclusions are only possible when the damping coefficient and mass is greater than zero.