Executive Programs

Workshops

Projects

Blogs

Careers

Placements

Student Reviews

For Business

Academic Training

Informative Articles

Find Jobs

We are Hiring!

All Courses

Choose a category

Mechanical

Electrical

Civil

Computer Science

Electronics

Offline Program

All Courses

CHOOSE A CATEGORY

Mechanical

Electrical

Civil

Computer Science

Electronics

Offline Program

Top Job Leading Courses

Automotive

CFD

FEA

Design

MBD

Med Tech

Courses by Software

Design

Solver

Automation

Vehicle Dynamics

CFD Solver

Preprocessor

Courses by Semester

First Year

Second Year

Third Year

Fourth Year

Courses by Domain

Automotive

CFD

Design

FEA

Tool-focused Courses

Design

Solver

Automation

Preprocessor

CFD Solver

Vehicle Dynamics

Machine learning

Machine Learning and AI

POPULAR COURSES

Post Graduate Program in Hybrid Electric Vehicle Design and Analysis

Post Graduate Program in Computational Fluid Dynamics

Post Graduate Program in CAD

Post Graduate Program in CAE

Post Graduate Program in Manufacturing Design

Post Graduate Program in Computational Design and Pre-processing

Post Graduate Program in Complete Passenger Car Design & Product Development

Executive Programs

Workshops

For Business

Success Stories

Placements

Student Reviews

Projects

Blogs

Academic Training

Find Jobs

Informative Articles

We're Hiring!

+91 9342691281 Log in

Calculation of Stiffness in Structural elements

Question 1: AIM - Compute lateral stiffness of the one story frame with an intermediate realistic stiffness of the beam. The system has 3 DOFs as shown. Assume L = 2h and Elb = Elc ANS - ASSUMING THE THREE DEGREE OF FREEDOM SYESTEM . CASE - 1 UNIT DISPLACEMENT u1=1 STIFFNESS…

Harshal virkhare
updated on 18 Jul 2022

Question 1:

AIM - Compute lateral stiffness of the one story frame with an intermediate realistic stiffness of the beam. The system has 3 DOFs as shown. Assume L = 2h and El_b= El_c

ANS - ASSUMING THE THREE DEGREE OF FREEDOM SYESTEM .

CASE - 1

UNIT DISPLACEMENT u1=1

STIFFNESS COEFFICEANT OF COLUMN TRANSLATION (2 SIMMILER)

= 2x 12EI/h

STIFFNESS COEFFICIENT OF BEAM ROTATION (2 END)

= EI/h^2

CASE - 2

UNIT ROTATION U2 - 1

STIFFNES COEFFICIENT OF COLUMN ROTATION AT RIGHT END

= 6EI/h^2

STIFFNES COEFFICIENT OF COLUMN + BEAM ROTATION AT LEFT END

= (4EI/h + 4EI/L)

= (4EI/h + 4EI/2h) = 6EI/h

CASE -3

UNIT ROTATION u3 =1

STIFFNESS COEFICIENT OF COLUMN ROTATION AT LEFT END

= 6EI/h^2

STIFFNESS COEFICIENT OF COLUMN + BEAM ROTATION AT RIGHT END

(4EI/h + 4EI /2h) = (6EI/h)

= [ 24EIc/h^3 6EIc/h^2 6EIc/h^2 ]

[ 6EIc/h^2 6EIc/h 6EIc/h ]

Fs = k.u

EIc/h^3 = [ 24 6h 6h ]

[ 6h 6h^2 h^2 ]

[ 6h h^2 6h^2 ]

by applying static condensation method , and deducing the three unknown expression in to 2 unknown equiation.

{u2}

{u3} = - [ 6h^2 h^2 ] ^-1 [6h] [1]

[h^2 6h^2 ] = [6h] = u1 = -(6/7H) [1] u1

fs ( 24ELc/h^3 - ELc/h^3 * 6/7h (6h 6h) [1] ) u1

[1]

= 96/7 ELc/h^3 u1

stiffnes is the ammounrt of the force required for unit displacement so interchanging the translation u1 to the left side, we are arrive the stiffnes coefficient as follow.

k= 96/7 ELc/Gh^3

ans .

AIM -

Question 2:

For the following structures:

Determine the number of degrees-of-freedom for dynamic analysis
Establish the equation of motion
Calculate their natural frequencies

ANS -

POSITION OF THE ELEMENT CAN BE DESCRIBE BY ONE COORDINATE ONLY.

1. number of degrees-of-freedom for dynamic analysis - the syestem has single degree of freedom structure.

2. Establish the equation of motion -

the column has fixed end at bottom, so the stiffnes coefficient will be as follow.

k = 3EI/H^3

THE EQUATION OF THE MOTION SHALL BE - MU + KU = 0

3. Calculate their natural frequencies - natural frequency formula ω = √ k/m

ω = √ 3EI/Mh^3

POSITION OF THE ELEMENT CAN BE DESCRIBED BY 1 CORDINATE ONLY u(t).

BECAUSE BEAM WITH INFINITE STIFFNES WILL INDUCE UNIFORM TRANSLATION IN ALL COLUMN

1. number of degrees-of-freedom for dynamic analysis - the syestem has single degree of freedom structure.

TWO COLUMN WITH BOTH END FIXED AND ONE COLUMN HAS PINNED FIXED END. SO THE STIFFNESS COFFICIENT WILL BE AS FOLLOW.

K1 = 12EI/h^3 K2 = 12EI/h^3 K3 = 12EI/h^3

for parallel stiffnes elements Ke = (k1+k2+k3) = 27ei/*h^3

THE EQUATION OF THE MOTION SHALL BE - MU + KU = 0

NATURAL FREQUENCY FORMULA -

ω = √ k/m

ω = √ 27EI/Mh^3

AIM -

Question 3:

Consider the propped cantilever shown in the figure below. The beams are made from the same steel section and have lengths as shown on the diagram. Determine the natural period of this system if a large mass, M, is placed at the intersection of the beams at point A. The weight of the beams in comparison with the mass M is very small.

ANS - 1. EFFECTIVE STIFFNES OF THE SYESTEM - Ke = Kb+Kc

KB = 48EI/lb^3

Kc = 3EI/lc^3

ke = 3EI (1/Lc^3 + 16/Lb^3)

NATURAL FREQUENCY FORMULA -

ω = √ k/m

ω = √3EI(1/Lc^3 + 16/Lb^3)/M

TIME PERIOD - T = 2π/ω $2^{3}$ $2^3$ ans .

AIM -

Question 4

Determine an expression for the effective stiffness of the following systems

ANS - A.

DETERMINNING THE EXPRESSION FOR THE EFFECTIVE STIFFNES FOR THREE ELEMENT WHICH IS SHOWN IN BELEOW.

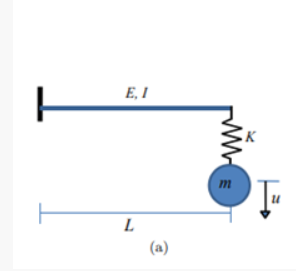
1. THE STIFFNESS COEFFICIENT FOR THE BEAM ELEMENT IS = 3EL/ $L^{3}$ $L^3$

2. THE STIFFNESS COEFFICIENT FOR THE SPRING IS 'K'

3.THE STIFFNESS ELEMENT ARE IN SEREIS SO.

$\frac{1}{K E}$ $1 /( KE$ = $\frac{L^{3}}{3 E I}$ $L^3/(3EI)$ + $\frac{1}{K}$ $1/K$

$\frac{1}{K E}$ $1 /( KE$ = $K L^{3} + 3 E \frac{I}{3 E I K}$ $KL^3+3 EI /( 3EIK$

Ke = $3 E I \frac{K}{K L^{3} + 3 E I}$ $3EIK/(KL^3+3EI$

ELEMENT (B.) ANS

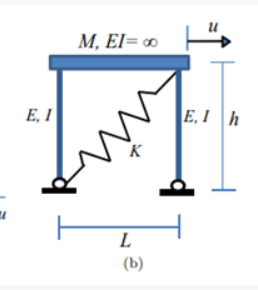
`. THE STIFFNESS COEFICIENT OF THE BOTH THE COLUMN ELEMENT IS $3 E \frac{I}{h^{3}}$ $3EI/h^3$

2. THE STIFFNESS COEFFICIENT FOR THE SPRING IS 'K' BUT IS INCLINED SO THE HORIZONTAL FORCE (P) AND DEFORMATION (U) HAS TO BE RESOLVED IN TO INCLINED COMPONENTS TO ARRIVE ACTUAL COEFFICIENT OF THE SPRING.

INCLINED COMPONENET OF LOAD 'P' = $\frac{P}{C O S \emptyset}$ $P/(COS emptyset$

inclined componenet of deformation'u' = u $C O S \emptyset$ $COS emptyset$ `

stiffness coefficient of spring $k = \frac{p}{u} {cos}^{2} \emptyset$ $k=p/ucos^2emptyset$

$\frac{p}{u} = k s = k {cos}^{2} \emptyset$ $p/u=ks=kcos^2emptyset$

$cos \emptyset = \frac{l}{{\sqrt{l}}^{2}} + h^{2}$ $cosemptyset=l/sqrtl^2+h^2$

${cos}^{2} \emptyset = \frac{l^{2}}{l^{2}} + h^{2}$ $cos^2emptyset=l^2/l^2+h^2$

Ks = K $\frac{l^{2}}{l^{2}} + h^{2}$ $l^2/l^2+h^2$ `

THE EFFECTIVE STIFFNESS OF THE SYESTEM = KE= $6 E \frac{I}{h^{3}} + k \frac{l^{2}}{l^{2}} + h^{2}$ $6EI/h^3+kl^2/l^2+h^2$ ANS.

ELEMENT (C) ANS -

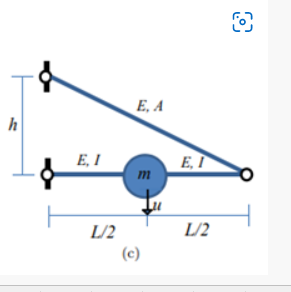
1. THE STIFFNESS COEFICIENT OF THE PINNED BEAM IS K1 = 48EI/L^3

2. THE EFFECTIVE STIFNESS COEFICIENT FOR THE SYESTEM HAS TO BE FORMED BY ADDING THE RELATIVE AXIAL STIFFNESS PROVIDED BY THE INCLINED STRUT CONNECTED AT THE RIGHT END.

3. FORCE ACTING AT THE RIGHT END IS' MG/2 'AND DEFORMATION CAUSED BY THE STRUT AT THE POINT OF 'M' IS HALF OF ITS RIGHT END NODEL DEFORMATION.

$m \frac{g}{2} = k e a . v e r t \cdot 2 \cdot △ 2$ $mg/2 =kea.vert *2*triangle2$

$m \frac{g}{2} = 4 . k e a . v e r t$ $mg/(2 )= 4.kea.vert$

$k 2$ $k2$ =4 kea.vert`

we assume vertical axial stiffness in our calculation.but we have in inclined axial stiffness in the given syestem so we have to resolve the (kea.vert) into (kea).

$k 2 = 4 k e a \frac{h^{2}}{h^{2}} + l^{2}$ $k2=4keah^2/h^2+l^2$

the effective stiffness shall be arive as . $\frac{1}{k} e = \frac{1}{k} 1 + \frac{1}{k} 2$ $1/ke=1/k1+1/k2$

` $\frac{1}{k} e = \frac{1}{48 E \frac{I}{L^{3}}} + \frac{1}{4 K e a \frac{h^{2}}{l^{2}} + h^{2}}$ $1/ke=1/(48EI/L^3)+1/(4Keah^2/l^2+h^2)$

$\frac{1}{k} e = \frac{1}{48 E \frac{I}{l^{3}}} + 1 - (4 E A \frac{h^{2}}{{(l^{2} + h^{2})}^{15}})$ $1/ke=1/(48EI/l^3)+1-(4EAh^2/(l^2+h^2)^15)$

$k e = (4 E A \frac{h^{2}}{{(l^{2} + h^{2})}^{3}} / 2) 48 E \frac{I}{l^{3}} / 4 E A h^{2} \frac{{(l^{2} + h^{2})}^{3}}{2} + 48 E \frac{I}{l^{3}}$ $ke=(4EAh^2/(l^2+h^2)^3/2)48EI/l^3/4EAh^2(l^2+h^2)^3/2+48EI/l^3$